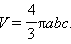Глава 7. Объемы и поверхности круглых тел
7.2. Вычисление объемов тел вращения
Укажем общий способ вычисления объемов тел вращения. В частности, вычислим объем шара и его частей.
 1
|
| Рисунок 7.2.1
|
Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox (рис. 7.2.1), вследствие чего образуется тело вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка. На промежутке (a; b) выберем точку x. Сечение, проведенное через эту точку перпендикулярно оси Ox, есть круг площадью S (x) = πf 2 (x). Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V.
Теорема 7.3.
Объем тела вращения равен
 2
|
| Рисунок 7.2.2
|
Придадим x приращение Δx > 0 (x + Δx < b). Построим два цилиндра с общей высотой Δx (рис. 7.2.2). Меньший цилиндр имеет своим основанием круг площадью S (x), а больший – круг площадью S (x + Δx). Если ΔV – прирост объема тела вращения, то S (x)Δx < ΔV < S (x + Δx)Δx, откуда
Поскольку функция f (x) непрерывна, то непрерывна и функция
следовательно,
Переходя к пределу в двойном неравенстве, имеем
то есть V' (x) = S (x).
Объем V (x) является первообразной для функции S (x) на промежутке [a; b]. Отсюда имеем
|
Теорема 7.4.
Объем шара равен 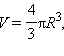 где R – радиус шара.
где R – радиус шара.
 3
|
| Рисунок 7.2.3
|
На рис. 7.2.3 изображена четверть круга радиуса R с центром в точке (R; 0). Уравнение окружности этого круга 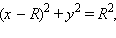 откуда
откуда 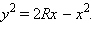 Функция
Функция 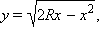 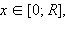 непрерывная, возрастающая, неотрицательная, следовательно, для нахождения объема тела вращения можно использовать предыдущую теорему. Вследствие вращения четверти круга вокруг оси Ox образуется полушар. Следовательно,
непрерывная, возрастающая, неотрицательная, следовательно, для нахождения объема тела вращения можно использовать предыдущую теорему. Вследствие вращения четверти круга вокруг оси Ox образуется полушар. Следовательно,
откуда 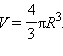
Заметим, что формула для объема шара следует из формулы для объема шарового сегмента при H = 2R.
|
В качестве тренировки докажите, что объем эллипсоида, задаваемого уравнением 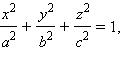 определяется формулой
определяется формулой
 4
|
| Рисунок 7.2.4
|










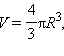 где
где 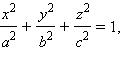 определяется формулой
определяется формулой