

 |
 |
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (~ 140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.

|
| Рисунок 1.24.1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд |
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном И. Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Т. Браге.
Первый закон Кеплера (1609 г.):
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
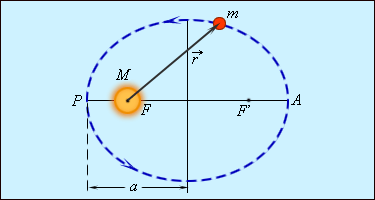
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка
|
| Рисунок 1.24.2. Эллиптическая орбита планеты массой |
Почти все планеты Солнечной системы (кроме Плутона) движутся по орбитам, близким к круговым.
Второй закон Кеплера (1609 г.):
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
Рис. 1.24.3 иллюстрирует 2-й закон Кеплера.
|
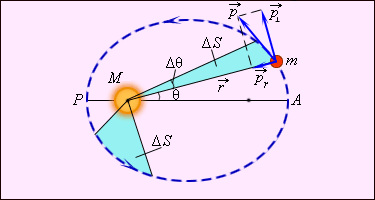
| Рисунок 1.24.3. Закон площадей – второй закон Кеплера |
Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рис. 1.24.3 изображен вектор импульса тела 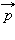 и его составляющие
и его составляющие 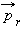 и
и 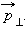 Площадь, заметенная радиус-вектором за малое время
Площадь, заметенная радиус-вектором за малое время
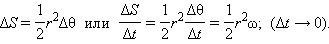 |
Здесь  – угловая скорость (см. §1.6).
– угловая скорость (см. §1.6).
Момент импульса 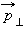 и
и 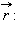
|
Из этих отношений следует:
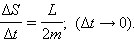 |
Поэтому, если по второму закону Кеплера 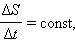 то и момент импульса
то и момент импульса
В частности, поскольку скорости планеты в перигелии 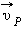 и афелии
и афелии 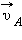 направлены перпендикулярно радиус-векторам
направлены перпендикулярно радиус-векторам 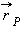 и
и 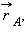 из закона сохранения момента импульса следует:
из закона сохранения момента импульса следует:
Третий закон Кеплера (1619 г.):
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:
|
Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше
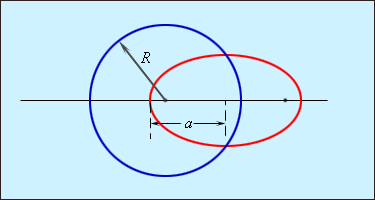
На рис. 1.24.4 изображены две орбиты, одна из которых – круговая с радиусом
|
| Рисунок 1.24.4. Круговая и эллиптическая орбиты. При |

 |
|
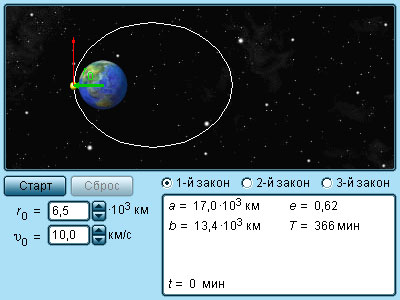
Модель.
Законы Кеплера
|
Несмотря на то, что законы Кеплера явились важнейшим этапом в понимании движения планет, они все же оставались только эмпирическими правилами, полученными из астрономических наблюдений. Законы Кеплера нуждались в теоретическом обосновании. Решающий шаг в этом направлении был сделан Исааком Ньютоном, открывшим в 1682 году закон всемирного тяготения:
|
Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что
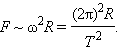 |
Если 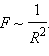
Свойство консервативности гравитационных сил (см. §1.10) позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.
Потенциальная энергия тела массы
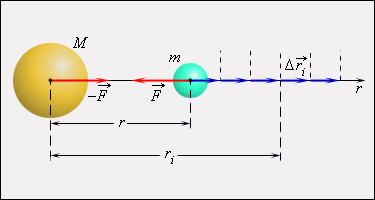
Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5).
|
| Рисунок 1.24.5. Вычисление потенциальной энергии тела в гравитационном поле |
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа 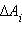 гравитационной силы
гравитационной силы 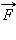 на малом перемещении
на малом перемещении 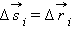 есть:
есть:
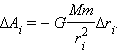 |
Полная работа при перемещении тела массой
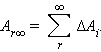 |
В пределе при
|
Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.
Если тело находится в гравитационном поле на некотором расстоянии
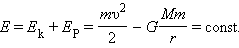 |
В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.
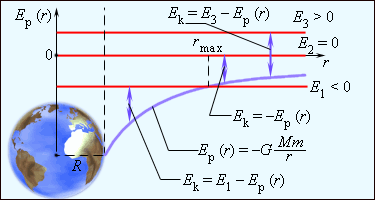
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6).
При
|
| Рисунок 1.24.6. Диаграмма энергий тела массой |
При
При
Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.
Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли.
|
Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.
|
Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна
 |
 |
 |

