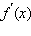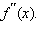Глава 3. Дифференцирование и интегрирование функций
3.2. Исследование функций при помощи производных
3.2.4. Построение графиков функций
Мы изучили графики элементарных функций. При построении графиков функций более сложного вида можно примерно придерживаться следующего плана.
- Найти область определения и область значений функции.
- Выяснить, является ли функция четной (нечетной).
- Выяснить, является ли функция периодической.
- Найти точку пересечения графика функции с осью ординат.
- Найти нули функции и промежутки знакопостоянства.
- Вычислить производную функции
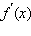и определить точки, в которых могут существовать экстремумы.
- Найти промежутки монотонности функции.
- Определить экстремумы функции.
- Вычислить вторую производную
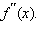
- Определить точки перегиба.
- Найти промежутки выпуклости функции.
- Найти асимптоты графика.
- Найти значения функции в нескольких контрольных точках.
- Построить эскиз графика функции.
Заметим, что при построении графиков элементарных функций иногда достаточно исследовать только несколько пунктов указанного плана.
 |
|
Модель 3.7.
Мастер построения графиков
|
Рекомендуется все найденные точки занести в таблицу:
| x |
(–∞; –2) |
–2 |
(–2; 1) |
1 |
(1; +∞) |
| y |
(+∞; 0) |
0 |
(0; +∞) |
∞ |
(–∞; 0) |
| f' (x) |
– |
0 |
+ |
∞ |
+ |
| f'' (x) |
+ |
2 |
+ |
∞ |
– |
| Примечание |
|
Минимум |
|
Асимптота |
|
|
| Таблица 3.2.4.1 |
