M.2.4. Тематическое поурочное планирование изучения алгебры и начал анализа (11 класс) по учебно-методическому комплекту М. И. Башмакова. (3 часа в неделю, общеобразовательный уровень)

Глава M. Методика

M.2. Примерное поурочное планирование

M.2.4. Тематическое поурочное планирование изучения алгебры и начал анализа (11 класс) по учебно-методическому комплекту М. И. Башмакова. (3 часа в неделю, общеобразовательный уровень)

Литература

Башмаков М. И. Алгебра и начала анализа. 10–11 кл.: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, 2001. – 400 с.
Программы для общеобразовательных школ, гимназий, лицеев: математика. 5–11. Г. М. Кузнецова. – М.: Дрофа, 2000. – 320 с.

№ урока	Содержание	Название модели курса, главы электронного учебника курса «Открытая Математика 2.6. Функции и Графики»	Вид проверочной работы
Показательная и логарифмическая функции (40 ч)
1	Степени с произвольным показателем		тренажеры
2–3	Свойства степеней	§ 2.4.2. Степенная функция (задача 3)	тренажеры, с/р
4–5	Лабораторная работа-исследование 5.4.	Графер
6–7	Свойства показательной функции	Графер, § 2.4.3. Показательная функция (задачи с решениями 4, 5)	с/р, л/р
8–9	Производная показательной функции
10	Число e
11–12	Логарифмы		тренажеры, с/р
13–14	Свойства логарифма		тренажеры
15	Модуль перехода
16–17	Свойства логарифмической функции	Графер, § 2.4.4. Логарифмическая функция (задачи с решениями 2, 3, 4, 5)	тренажеры, тесты, с/р, л/р
18–19	Производная логарифмической функции		тесты
20–23	Вычисление логарифмов
24	Контрольная работа №1
25–27	Простейшие уравнения		тренажеры, тесты, с/р
28–30	Простейшие неравенства		тренажеры, с/р
31–32	Введение новой неизвестной
33	Задачи на исследование функций. с. 366–368, № 26–40
34–35	Использование свойств монотонности при решении показательных уравнений	Графер. Решение уравнений § 2.5.1. Решение уравнений (вопросы, задачи с решениями)	тесты
36	Определение. Графики взаимно-обратных функций	Модель 1.11. Обратные функции
37	Условие существования обратной функции. Графики взаимно-обратных функций	§ 1.3.9. Обратная функция (вопросы, задачи)
38	Свойства взаимно-обратных функций. Условие существования обратной функции
39	Производная обратной функции. Свойства взаимно-обратных функций
40	Контрольная работа		2

№ урока	Содержание	Название модели курса, главы электронного учебника курса «Открытая Математика 2.6. Функции и Графики»	Вид проверочной работы
Уравнения и неравенства (34 ч)
41–42	Выражения		тренажеры, с/р
43–45	Уравнения	Модель 2.17. Решение уравнений	тесты
46	Равносильность		тренажеры, тесты
47–48	Тождества		тренажеры, с/р
49–50	Неравенства	Модель 2.19. Решение неравенств	тренажеры
51–52	Параметры	§ 2.5.1. Решение уравнений (задачи 2, 3, 4); § 2.2.3. График квадратичной функции (задачи с проверкой)
53	Общие приемы		тренажеры, тесты
54–56	Примеры решения уравнений. Урок-практикум		тренажеры
57–59	Алгебраические уравнения		тренажеры, с/р, и/с
60	Приближенные методы вычисления корней	Модель 2.18. Метод деления отрезка пополам	л/р
61–62	Общие приемы		тренажеры, тесты
63–65	Примеры решения неравенств	Модель 2.21. Система уравнений с двумя переменными	тренажеры, с/р, и/с
66	Доказательство неравенств		тренажеры
67–68	Способ подстановки		с/р
69–70	Лабораторная работа «Графическое решение систем уравнений»	Графер
71	Симметричные системы
72–73	Линейные системы		с/р
74	Контрольная работа		2

№ урока	Содержание	Название модели курса, главы электронного учебника курса «Открытая Математика 2.6. Функции и Графики»	Вид проверочной работы
Интеграл и его применение (10 ч)
75	Первообразная	§ 3.3.1. Первообразная	тренажеры, с/р
76–77	Теорема Ньютона-Лейбница	Модель 3.8. Дифференцирование и интегрирование функций, § 3.3.3. Основные приемы интегрирования, § 3.4.3. Формула Ньютона-Лейбница
78	Свойства интеграла	Модель 3.10. Свойства определенного интеграла, § 3.4.2. Свойства определенного интеграла
79–80	Площадь	§ 3.4.4. Геометрические приложения определенного интеграла, модель 3.9. Определенный интеграл	тренажеры, тесты, с/р
81–82	Схема применения интеграла
83	Контрольная работа		1
Повторение (18 ч)

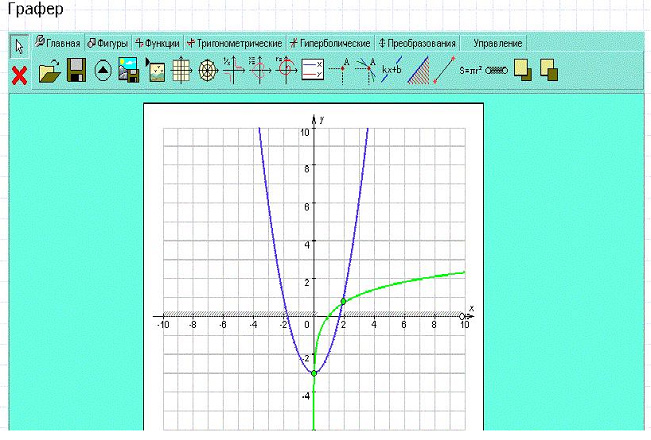
Графер – интерактивная модель, многообразие функций делают ее незаменимым помощником учителя. Используя «Графер» можно строить графики алгебраических, параметрических и тригонометрических функций в декартовой и полярной системе координат, исследовать функцию по графику. С помощью программы легко определить координаты точек пересечения графиков, построить касательную в заданной точке. Выделяет полуплоскость, интервал, отрезок на плоскости.

Например, можно решить неравенство x² – 3 > ln x с помощью компьютерного моделирования.

Рисунок M.2.4.1

Примечание. Звездочкой (*) отмечен необязательный, дополнительный материал.